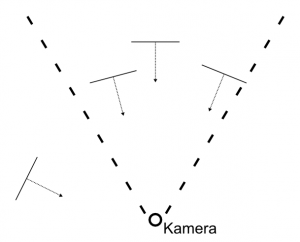Einfach ausgedrückt sind Billboards flächige grafische Elemente die immer zum Betrachter ausgerichtet sind. In der Computergrafik werden sie verwendet um Partikeleffekte wie Rauch oder Feuer mit moderatem Rechenaufwand darzustellen oder auch um bei weit entfernten Objekten anstelle eines aufwändigen 3D Modelles nur noch ein „Bild“ des Modells anzuzeigen.

Will man nun Billboards selbst implementieren gibt es mehrere Varianten zur Auswahl, eine davon möchte ich jetzt kurz vorstellen.

Bitte die Quellenangaben am Endes des Textes beachten!

Eine Möglichkeit, ist die, die oben im Bild gezeigt wird. Die Billboard Objekte drehen sich immer so, das sie genau zur Kamera zeigen (eine weitere Variante wäre es alle Objekte so auszurichten das sie in die negative Blickrichtung der Kamera zeigen).

Bei der oben gezeigten Methode gibt es nun auch wieder mehrere Möglichkeiten wie die Objekte ausgerichtet werden. Will man beispielsweise einen Wald darstellen ist es ausreichen wenn die Billboards sich nur um die senkrecht stehende Achse drehen und nicht auch noch zum Betrachter neigen. Bei vielen Effekten wie z.B. Rauch ist es dagegen sehr viel sinnvoller, wenn die Objekte immer auch der Kameraneigung folgen, sodass man immer genau auf die Fläche des Objektes schaut. Wie man für beide Varianten die benötigten Daten erhält erkläre ich im folgenden:

Variante 1: Rotation um die senkrechte Achse (Beispiel: Wald)

Für diesen Fall gehen wir davon aus, das wir irgendwo in unserer virtuellen Welt ein Billboard Objekt haben das in Höhe und Breite (x und y Koordinaten) eine Ausdehnung hat und in der Tiefe nicht. Ausserdem ist das Objekt so ausgerichtet das die Oberfläche (Oberflächennormale) in Richtung der negativen Tiefen-Aches (z Koordinate) zeigt.

 

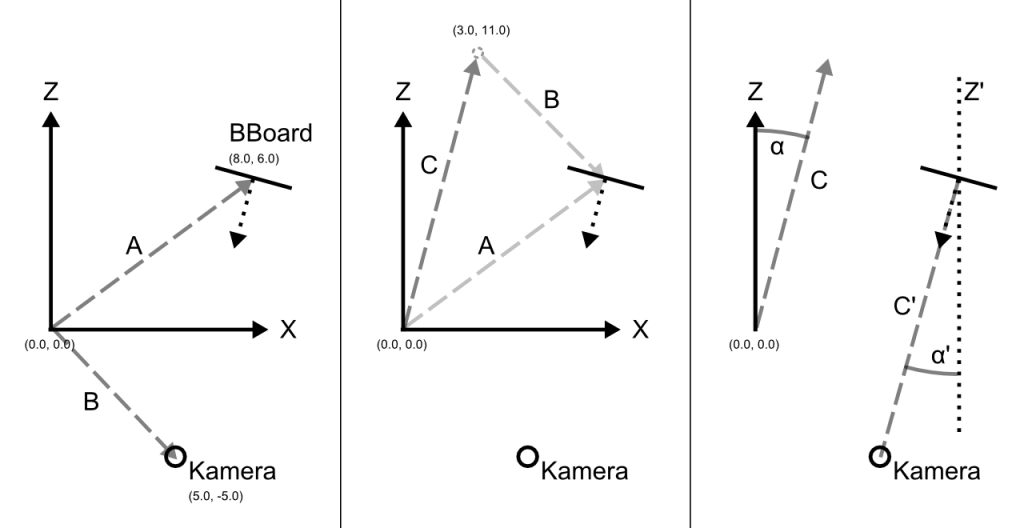
In der obigen Abbildung ist das ganze aus der „Vogelperspektive“ zu sehen, daher ist die Y-Achse (die „Höhe“) nicht zu sehen, da man von oben darauf schaut. Dementsprechend sind die Koordinaten auch nur für die X und Z-Achse angegeben.

Links: Gezeigt sind die Kamera an Position (5.0, -5.0) und ein Billboard an (8.0, 6.0). A und B sind Vektoren die der Verschiebung der beiden Objekte vom Ursprung (0.0, 0.0) an ihre aktuelle Position entsprechen.

Was wir nun benötigen ist ein Winkel um den das Billboard Objekt um die Y-Achse (die senkrecht stehende Achse) gedreht werden muss, sodass es in Richtung der Kamera zeigt.

Glücklicherweise gibt es dafür bereits seit geraumer Zeit die „atan2“ Funktion die in diversen Programmiersprechen zur Verfügung steht. Die Funktion berechnet mit dem Aufruf „atan2(y,x)“ den Winkel des Vektors (x,y) zur positiven X-Achse. Wir benötigen also nur noch einen Vektor der von der Kamera zum Billboard Objekt zeigt und können mit diesem den gesuchten Winkel berechnen.

Mitte: Hier sehen wir dann auch wie wir den benötigten Vektor bekommen. Gesucht ist C, das der Verbindung von Kamera und Billboard entspricht. C ergibt sich einfach indem wir gemäß der normalen Vektorsubtraktion den Endpunkt vom Anfangspunkt subrahieren: C = (A – B)

Die konkreten Werte für das Beispiel:

C = (8.0, 6.0) – (5.0, -5.0) = (8.0 – 5.0, 6.0 – (-5.0)) = (3.0, 11.0);

Rechts: Aus dem nun berechneten C lässt sich der Winkel α nun mit der atan2 Funktion berechnen (Darauf achten, das der Aufruf von atan2 mit y, x erfolgt. Da wir hier die x und z Koordinaten verwenden ist der Aufruf atan2(x,z), wir bekommen also den Winkel zur Z-Achse!):

atan2(3.0, 11.0) = 0.266252 rad

Für das Objekt das in Richtung der negativen Z-Achse (Z‘ in der Abbildung) zeigt, bedeutet das nun, dass es um α‘ = 15.255° (Umgerechnet vom Bogenmaß) gedreht werden muss.

Diese recht lange Erklärung lässt sich dann schlussendlich auch sehr stark verkürzen, wenn die Methode eingesetzt wird. Am Beispiel von C++ und DirectX sieht das ganze dann so aus:

winkel = atan2(bboard.x - kamera.x, bboard.z - kamera.z);
D3DXMatrixRotationY(&worldMatrix, winkel);
D3DXMatrixTranslation(&positionsMatrix, bboard.x, bboard.y, bboard.z);
D3DXMatrixMultiply(&worldMatrix, &worldMatrix, &positionsMatrix);

Erklärung: Zuerst wird der Winkel entsprechend dem beschriebenen Verfahren berechnet. bboard und kamera sind dabei Variablen die die Positionen der beiden Objekte beinhalten deren Komponenten über .x, .y und .z angesprochen werden können.

Danach wird mit D3DXMatrixRotationY eine Rotationsmatrix erstellt die genau der Drehung des berechneten Winkels um die Y-Achse entspricht (Da die Welt-Matrix, worldMatrix, hier der Einheitsmatrix entspricht).

D3DMatrixTranslation erstellt dann eine Matrix die die Verschiebung des Billboards an seine tatsächliche Position bewirkt und mit D3DXMatrixMultiply werden die Rotations- und die Verschiebungsmatrix dann kombiniert. Damit steht für das Rendern dann eine Matrix zur Verfügung die das Billboard an seiner Position so um die Hochachse dreht, das es immer zur Kamera zeigt.

Variante 2: Fläche zeigt immer zur Kamera (Beispiel: Rauch)

Vom theoretischen Hintergrund ist diese zweite Variante etwas komplexer da sie ein tieferes Verständnis der Vorgänge beim Rendern von Computergrafik benötigen.

So sollten die Begriffe „Welt-Matrix“ und „View-Matrix“ klar sein um zu verstehen warum diese Methode funktioniert.

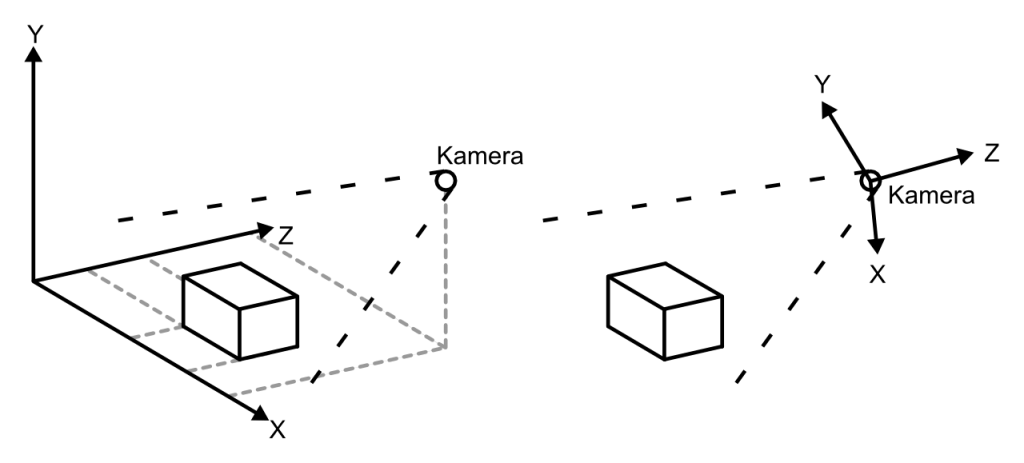Obige Abbilung zeigt dabei schematisch den Unterschied bzw. die Funktion beider Matrizen. Aufgabe dieser Matrizen ist es eine Umrechnung zwischen Koordinatensystem zur Verfügung zu stellen sodass man die Position von Objekten im Raum definieren kann.

Die Welt-Matrix ist dafür zuständig die Koordinaten alle Objekte in einen einheitlichen Raum zu bringen (3D Modelle verwenden lokale Koordinatensysteme, diese müssen so umgerechnet werden das sich hinterher alle Objekte in einem Koordinatenraum befinden entsprechend der Positionen an denen sie sich befinden sollen).

Um aber nun Objekte aus der Sicht einer virtuellen Kamera darstellen zu können müssen wir wissen wie die Objekte in Relation zur Kamera stehen. Dazu benötigen wir eine Matrix die die Koordinaten aus der „Welt-Sicht“ in die „Kamera-Sicht“ transformiert. Diese Matrix ist die View-Matrix. Wenden wir sie an, ist der Ursprung des Koordinatensystem nun die Position der Kamera und alle Objektpositionen berechnen sich von diesem Ursprung aus. Da die Berechnung und Bedeutung der View-Matrix sehr komplex ist kann ich an dieser Stelle leider nicht weiter darauf eingehen, es empfiehlt sich in der gängigen Fachliteratur oder im Netz weitere Informationen einzuholen.

Um nun ein Billboard mit Hilfe dieser Matrix zu platzieren muss man ein wenig vom Ergebnis zurückdenken: Das Ziel ist es ein Objekt zu bekommen das genau zur Kamera hin ausgerichtet ist. Das heißt also das es, aus Sicht der Kamera, eine Ausdehnung entlang der X und Y-Achsen haben darf und entlang der negativen Z-Achse ausgerichtet ist.

Zu diesem Objekt wollen wir nun wissen wie wir es vor der Anwendung der View-Matrix positionieren müssen damit es richtig angezeigt wird. Dazu müssen wir die Umkehrung der View-Matrix berechnen, also die Inverse. Da die Inverse aber sehr komplex ist, würde das, gerade bei vielen Objekten, ein Performanceproblem darstellen. Glücklicherweise benötigen wir nur die Rotation, die wir sehr viel einfacher aus der transponierten View-Matrix bekommen.

Um also nun unser Billboard richtig zu positionieren und zu drehen benötigen wir lediglich den Rotationsanteil aus der transponierten View-Matrix (der Rotationsanteil ist eine 3×3 Matrix aus der 4×4 View-Matrix, im Prinzip werden die vierte Zeile und Spalte abgeschnitten. Das funktioniert allerdings nur solange es keine Skalierung in der View-Matrix gibt, da diese auf der Diagonalen der Matrix hinterlegt ist. In vielen Fällen kann man einfach die komplette transponierte View-Matrix nehmen, man kann aber sicherheitshalber die nicht relevante vierte Zeile und Spalte auf 0 setzen, und das letzte Elemente auf 1. Mehr zu den einzelnen Teilen der Matrix gibt es hier)! Als Codebeispiel könnte das nun so aussehen:

D3DXMatrixTranspose(&transponierteViewMatrix, &viewMatrix);
transponierteViewMatrix.m[0][3] = 0;
transponierteViewMatrix.m[1][3] = 0;
transponierteViewMatrix.m[2][3] = 0;
transponierteViewMatrix.m[3][0] = 0;
transponierteViewMatrix.m[3][1] = 0;
transponierteViewMatrix.m[3][2] = 0;
transponierteViewMatrix.m[3][3] = 1;
D3DXMatrixMultiply ( &worldMatrix, &worldMatrix, &transponierteViewMatrix);
D3DXMatrixMultiply ( &worldMatrix, &worldMatrix, &positionsMatrix );

D3DXMatrixTranspose speichert die transponierte View-Matrix in der Variable transponierteViewMatrix und die nicht relevanten Elemente werden auf 0, bzw. das letzte Element auf 1 gesetzt. Danach wird mit D3DXMatrixMultiply diese mit der Welt-Matrix verrechnet. Zuletzt wird die Position des Objektes in der Matrix positionsMatrix ebenfalls in die Welt-Matrix eingerechnet. Damit enthält die Welt-Matrix nun alle Transformationen die nötig sind um das Billboard korrekt anzuzeigen.

Anmerkung: Mit der ersten Variante ist es auch möglich das Billboard auf allen Achsen korrekt auszurichten, dafür muss man lediglich nach dem gleichen Schema auch einen Winkel um die X-Achse berechnen. Allerdings liegt das Objekt dann nicht immer senkrecht ausgerichtet in der Bildebene sondern ist eventuell um die Sichtachse gedreht!

Anmerkung 2: Um vor allem bei Partikeleffekten etwas mehr Varianz in die Darstellung vieler Billboards zu bekommen kann man einen zusätzlichen Rotationswert (die variable rotationsWinkel im folgenden Beispiel) um die Z-Achse einbringen:

D3DXMatrixTranspose(&transponierteViewMatrix, &viewMatrix);
D3DXMatrixRotationZ ( &rotationsMatrix, rotationsWinkel );
D3DXMatrixMultiply ( &worldMatrix, &worldMatrix, &rotationsMatrix );
D3DXMatrixMultiply ( &worldMatrix, &worldMatrix, &transponierteViewMatrix);
D3DXMatrixMultiply ( &worldMatrix, &worldMatrix, &positionsMatrix);

Quellen:

• Rastertek DirectX Tutorials, eine sehr gute Quelle für grundlegendes DirectX Wissen. Für die Variante 1 die hier vorgestellt wurde diente das DirectX 11 Kapitel 34 als Grundlage.
• Swiftcoder beschreibt die Matrizenoperationen um an die gesuchte Matrix aus Variante 2 zu kommen.